LeanAgent: Lifelong Learning for Formal Theorem Proving

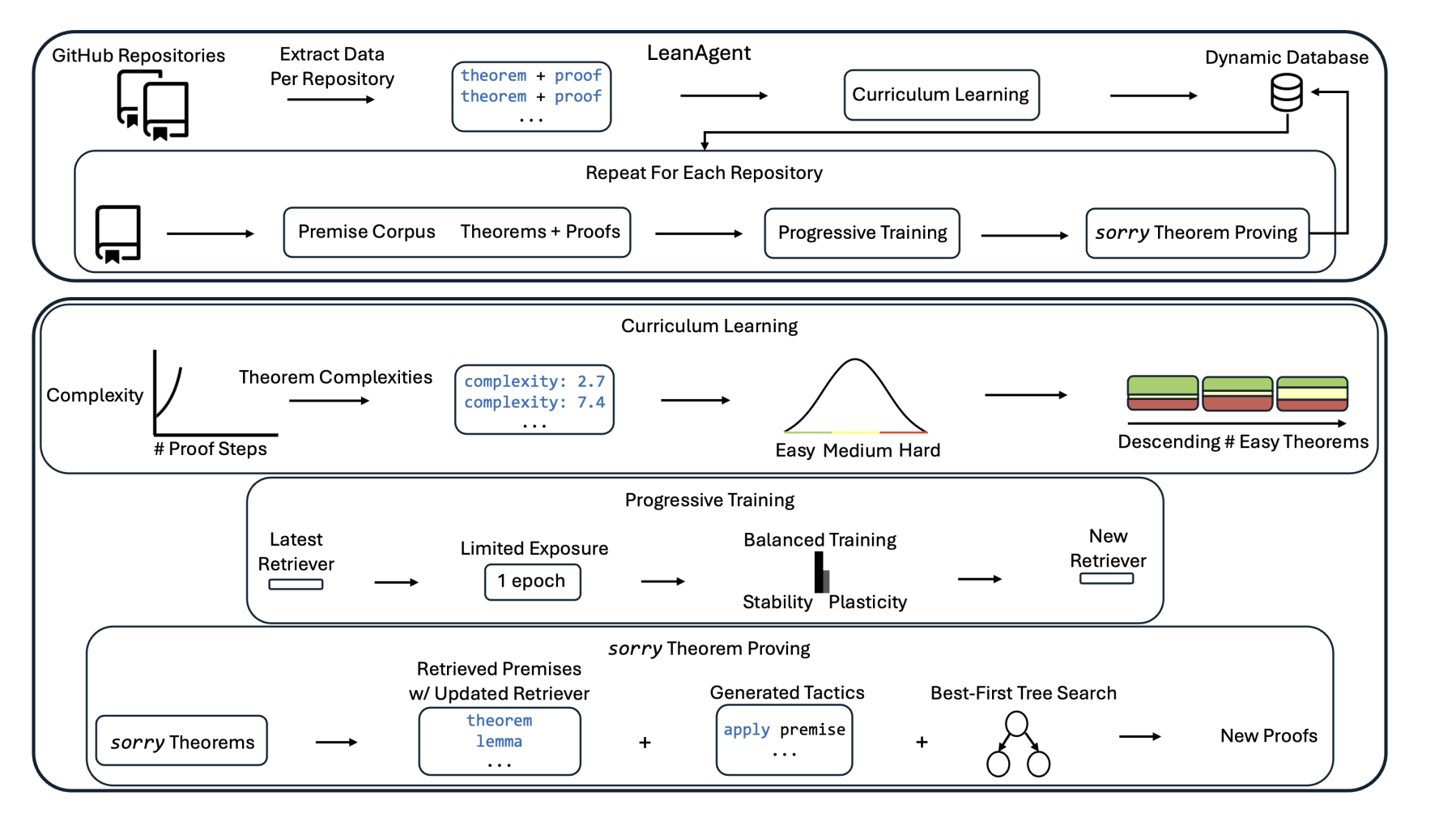
LeanAgent Overview

LeanAgent overview. LeanAgent searches for Lean repositories and uses LeanDojo to extract theorems and proofs. It uses curriculum learning, computing theorem complexity as e^S (S = proof steps) and calculating the 33rd and 67th complexity percentiles across all theorems to sort repositories by easy theorem count. LeanAgent adds the curriculum to its dynamic database. As a retrieval-based framework, LeanAgent generates a dataset (premise corpus and a collection of theorems and proofs) for each repository in the curriculum and progressively trains its retriever. Progressive training happens over one epoch to prevent forgetting old knowledge. Then, LeanAgent uses the updated retriever in a search-based method to generate formal proofs for theorems where formal proofs were previously missing, known as sorry theorems. It adds new proofs to the database.

Key Results

LeanAgent successfully generates formal proofs for 155 theorems across 23 diverse Lean repositories where formal proofs were previously missing, many from advanced mathematics including abstract algebra, algebraic topology, and complex analysis. It significantly outperforms static baselines like ReProver, demonstrating clear progression from basic concepts to advanced topics. Key repositories include the Polynomial Freiman-Ruzsa Conjecture, Hairy Ball Theorem, Coxeter groups, and scientific computing frameworks.

Abstract

Large Language Models (LLMs) have been successful in mathematical reasoning tasks such as formal theorem proving when integrated with interactive proof assistants like Lean. Existing approaches involve training or fine-tuning an LLM on a specific dataset to perform well on particular domains, such as undergraduate-level mathematics. These methods struggle with generalizability to advanced mathematics. A fundamental limitation is that these approaches operate on static domains, failing to capture how mathematicians often work across multiple domains and projects simultaneously or cyclically. We present LeanAgent, a novel lifelong learning framework for formal theorem proving that continuously generalizes to and improves on ever-expanding mathematical knowledge without forgetting previously learned knowledge. LeanAgent introduces several key innovations, including a curriculum learning strategy that optimizes the learning trajectory in terms of mathematical difficulty, a dynamic database for efficient management of evolving mathematical knowledge, and progressive training to balance stability and plasticity. LeanAgent successfully generates formal proofs for 155 theorems across 23 diverse Lean repositories where formal proofs were previously missing, many from advanced mathematics. It performs significantly better than the static LLM baseline, proving challenging theorems in domains like abstract algebra and algebraic topology while showcasing a clear progression of learning from basic concepts to advanced topics. In addition, we analyze LeanAgent's superior performance on key lifelong learning metrics. LeanAgent achieves exceptional scores in stability and backward transfer, where learning new tasks improves performance on previously learned tasks. This emphasizes LeanAgent's continuous generalizability and improvement, explaining its superior theorem-proving performance.

Key Innovations

Curriculum Learning Strategy

LeanAgent employs a sophisticated curriculum learning approach that uses theorem complexity based on e^S (where S is the number of proof steps) to order repositories by difficulty. It calculates the 33rd and 67th complexity percentiles to categorize theorems as easy, medium, or hard, then sorts repositories by their count of easy theorems to create an optimal learning trajectory.

Dynamic Knowledge Database

The system maintains a comprehensive dynamic database that tracks repository metadata, theorem categorization (proven, sorry proven, sorry unproven), premise files with imports, traced files, and detailed theorem information including proof states. This enables efficient reuse and management of evolving mathematical knowledge across repositories.

Progressive Training Architecture

LeanAgent implements progressive training that incrementally trains the retriever on newly generated datasets for exactly one epoch per repository to prevent catastrophic forgetting. This approach balances stability (retaining old knowledge) with plasticity (learning new concepts), achieving superior performance on lifelong learning metrics including backward transfer.

Best-First Tree Search with Retrieval

For sorry theorem proving, LeanAgent uses a best-first tree search that generates tactic candidates at each step, retrieves relevant premises based on similarity to the current proof state, and applies dependency filtering to ensure only accessible premises are considered. The search continues until a proof is found or the 10-minute time limit is reached.

Technical Architecture & Results

Experimental Setup

LeanAgent was evaluated on 23 diverse Lean repositories including advanced mathematical domains such as the Polynomial Freiman-Ruzsa Conjecture, Hairy Ball Theorem (algebraic topology), Coxeter groups, Mathematics in Lean textbook, scientific computing (SciLean), Carleson's Theorem, and various olympiad-style problems (MiniF2F). The system uses ReProver's retriever as the starting point and progressively trains on each repository for one epoch.

Performance Results

LeanAgent successfully proved 155 sorry theorems across the 23 repositories, significantly outperforming the static ReProver baseline. Notable achievements include proving theorems in advanced abstract algebra (Wedderburn's Little Theorem), algebraic topology (Hairy Ball Theorem components), complex analysis, and successfully handling the challenging PFR repository where it was the only system to prove theorems. The system demonstrated clear progression from basic arithmetic to advanced mathematical concepts.

Lifelong Learning Analysis

LeanAgent achieved exceptional performance on six lifelong learning metrics: superior Windowed-Forgetting (75.34% lower than alternatives), excellent Catastrophic Forgetting Resilience (0.88), and positive Expanded Backward Transfer (1.21), indicating that learning new tasks actually improved performance on previously learned tasks. This demonstrates LeanAgent's continuous generalizability and improvement capabilities.

Repository-Specific Insights

Mathematics in Lean Source: 72.4% accuracy (21/29 theorems), progressing from basic algebraic structures to advanced quantifier manipulation and set theory. SciLean: 9.2% accuracy (27/294 theorems), advancing from fundamental operations to sophisticated function spaces and abstract algebraic structures. MiniF2F: 24.4% accuracy (99/406 theorems), improving from basic arithmetic to complex induction and advanced number theory. PFR: Only system to prove theorems (2.7% accuracy), demonstrating unique capability in advanced mathematical research.

Impact & Future Directions

Contributions to Formal Mathematics

LeanAgent represents a significant step toward practical AI assistance in formal mathematics. By successfully proving previously unproven theorems across diverse repositories, it demonstrates the potential for AI systems to contribute meaningfully to mathematical research. The system discovered 7 exploits within Lean's type system and has contributed proofs back to the mathematical community through pull requests to repository maintainers.

Broader Applications

The lifelong learning framework extends beyond theorem proving to any domain requiring continuous knowledge accumulation without catastrophic forgetting. Potential applications include software verification, automated reasoning in legal systems, and scientific hypothesis generation. The approach of combining curriculum learning with progressive training offers a template for building robust AI systems that can adapt to evolving knowledge domains.

Future Research Directions

Future work could explore integration with interactive proof assistants like Lean Copilot for real-time assistance, incorporation of reinforcement learning for synthetic data generation during curriculum construction, and extension to additional mathematical libraries and theorem provers. The framework's modular design allows for integration with various large language models and search strategies, opening possibilities for more sophisticated reasoning architectures.